Trigonometric Identities: Formulas, Examples & Proofs

Trigonometric identities

Trigonometric identities are the building blocks of trigonometry, a branch of mathematics that explores the connections between angles and sides in triangles. These identities are equations involving trigonometric functions like sine, cosine, and tangent, and they hold true for any value of the variables used.

Basics of Trigonometric identities

These identities are incredibly helpful for simplifying complex expressions, solving equations, and proving theorems across science and engineering disciplines. Mastering their properties and uses is crucial for students and professionals in fields like math, physics, and engineering.

Trigonometric Identities PDF: Your Essential Math Resource

Understanding the Basics:

Trigonometric identities are fundamental equations that hold true for all values of the variables involved.
A comprehensive PDF provides a readily accessible reference for these crucial formulas.
These PDFs often include Pythagorean, reciprocal, and quotient identities, which are essential for simplifying complex trigonometric expressions.

Practical Applications:

A “Trigonometric Identities PDF” is invaluable for students and professionals in fields like mathematics, physics, and engineering.
They aid in solving equations, proving theorems, and simplifying calculations.
Having a downloadable PDF allows for offline access, making it a convenient study aid.

Download Trigonometric Identities PDF

List of Trigonometric Identities

Trigonometric identities connect the six main trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. Below, we’ll explore these identities in detail to understand how they work and how they’re used. Do you want Trigonometric identities mcqs?

Fundamental law of trigonometry
Reciprocal trigonometric Identities
Ratio trigonometric Identities
Pythagorean trigonometric Identities
Opposite Angle trigonometric Identities
Complementary Angle trigonometric Identities
Supplementary Angle trigonometric Identities
Sum and Difference trigonometric Identities
Periodic trigonometric Identities
Double Angle and Half Angle trigonometric Identities
Triple Angle trigonometric Identities
Sum to Product trigonometric Identities
Product to SUM trigonometric Identities
Sine Law and Cosine Law

Fundamental law of trigonometry

For this, we should know the formula to find the distance between two points in a plane.
Let $P(x_1, y_1)$ and $Q(x_2, y_2)$ be two points. If “d” denotes the distance between them, then,
$d = \sqrt{PQ} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
i.e., the square root of the sum of the square of the difference of x-coordinates and the square of the difference of y-coordinates.

Example 1:

Find the distance between the following points:

i) $A(3,8)$ , $B(5,6)$
ii) $P(\cos x, \cos y)$ , $Q(\sin x, \sin y)$

Solution:

i) Distance
$|AB| = \sqrt{(3-5)^2 + (8-6)^2} = \sqrt{4+4} = \sqrt{8} = 2\sqrt{2}$
$|AB| = \sqrt{(5-3)^2 + (6-8)^2} = \sqrt{4+4} = \sqrt{8} = 2\sqrt{2}$
ii) Distance
$\sqrt{(\cos x - \sin x)^2 + (\cos y - \sin y)^2}$

Example 2: Find the value of $\cos\frac{\pi}{12}$

Solution:

$\frac{\pi}{12} = 15^\circ = 45^\circ - 30^\circ = \frac{\pi}{4} - \frac{\pi}{6}$

$\cos\frac{\pi}{12} = \cos\left(\frac{\pi}{4} - \frac{\pi}{6}\right) = \cos\frac{\pi}{4}\cos\frac{\pi}{6} + \sin\frac{\pi}{4}\sin\frac{\pi}{6}$

$= \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2} + \frac{1}{\sqrt{2}} \cdot \frac{1}{2} = \frac{\sqrt{3} + 1}{2\sqrt{2}}$

Reciprocal trigonometric Identities

Sine, cosine, and tangent each have a reciprocal function: cosecant (reciprocal of sine), secant (reciprocal of cosine), and cotangent (reciprocal of tangent).

$\sin \theta = \frac{1}{\csc \theta}$ and $\csc \theta = \frac{1}{\sin \theta}$

$\cos \theta = \frac{1}{\sec \theta}$ and $\sec \theta = \frac{1}{\cos \theta}$

$\tan \theta = \frac{1}{\cot \theta}$ and $\cot \theta = \frac{1}{\tan \theta}$

Reciprocal Trigonometric Identities: Solved Examples

Reciprocal Trigonometric Identities: Solved Examples

Question 1: If $\cos \theta = \frac{4}{5}$ , find $\sec \theta$ .

Solution:

$\begin{align*} \sec \theta &= \frac{1}{\cos \theta}\\ &= \frac{1}{\frac{4}{5}}\\ &= \frac{5}{4} \end{align*}$

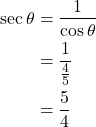
Question 2: If $\sin \alpha = -\frac{1}{2}$ , and $\alpha$ is in the third quadrant, find $\csc \alpha$ .

Solution:

$\begin{align*} \csc \alpha &= \frac{1}{\sin \alpha} \\ &= \frac{1}{-\frac{1}{2}} \\ &= -2 \end{align*}$

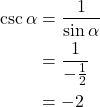
Question 3: If $\tan \beta = -\sqrt{3}$ , and $\beta$ is in the second quadrant, find $\cot \beta$ .

Solution:

$\begin{align*} \cot \beta &= \frac{1}{\tan \beta} \\ &= \frac{1}{-\sqrt{3}} \\ &= -\frac{\sqrt{3}}{3} \end{align*}$

Question 4: Simplify the expression: $\sin x \cdot \sec x$

Solution:

$\begin{align*} \sin x \cdot \sec x &= \sin x \cdot \frac{1}{\cos x} \\ &= \frac{\sin x}{\cos x} \\ &= \tan x \end{align*}$

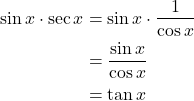
Question 5: Given that $\csc \theta = \frac{13}{5}$ and $\theta$ is an acute angle, find the values of all other trigonometric functions.

Solution:

Since $\csc \theta = \frac{13}{5}$ , $\sin \theta = \frac{1}{\csc \theta} = \frac{5}{13}$ .

Using the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$ :

$\begin{align*} \left(\frac{5}{13}\right)^2 + \cos^2 \theta &= 1 \\ \frac{25}{169} + \cos^2 \theta &= 1 \\ \cos^2 \theta &= 1 - \frac{25}{169} \\ \cos^2 \theta &= \frac{144}{169} \\ \cos \theta &= \frac{12}{13} \quad \text{(positive because $\theta$ is acute)} \end{align*}$

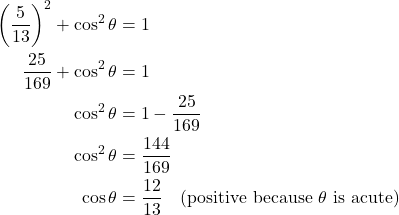
Now we can find the other functions:

$\begin{align*} \sec \theta &= \frac{1}{\cos \theta} = \frac{13}{12} \\ \tan \theta &= \frac{\sin \theta}{\cos \theta} = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12} \\ \cot \theta &= \frac{1}{\tan \theta} = \frac{12}{5} \end{align*}$

Reciprocal Trigonometric Identities: MCQs with explanations

Master Reciprocal Trigonometric Identities: 5 Key MCQs with Explanations

Reciprocal trigonometric identities are fundamental tools in trigonometry. They establish the relationship between the primary trigonometric functions (sine, cosine, tangent) and their reciprocals (cosecant, secant, cotangent). Test your knowledge with these 5 MCQs and get clear explanations to solidify your understanding.

MCQs:

Which of the following is the reciprocal identity for sine (sin θ)?

a) cos θ

b) tan θ

c) csc θ

d) sec θ

Explanation: The reciprocal of sine (sin θ) is cosecant (csc θ). Therefore, csc θ = 1/sin θ. The correct answer is c) csc θ.
If sin θ = 3/5, what is the value of csc θ?

a) 5/3

b) 3/5

c) 4/5

d) 5/4

Explanation: Since csc θ = 1/sin θ, if sin θ = 3/5, then csc θ = 1/(3/5) = 5/3. The correct answer is a) 5/3.
Which of the following is the reciprocal identity for cosine (cos θ)?

a) cot θ

b) sec θ

c) csc θ

d) tan θ

Explanation: The reciprocal of cosine (cos θ) is secant (sec θ). Therefore, sec θ = 1/cos θ. The correct answer is b) sec θ.
If cos θ = 1/2, what is the value of sec θ?

a) 1/2

b) 2

c) √3/2

d) 2/√3

Explanation: Since sec θ = 1/cos θ, if cos θ = 1/2, then sec θ = 1/(1/2) = 2. The correct answer is b) 2.
Which of the following is the reciprocal identity for tangent (tan θ)?

a) sec θ

b) csc θ

c) cot θ

d) sin θ

Explanation: The reciprocal of tangent (tan θ) is cotangent (cot θ). Therefore, cot θ = 1/tan θ. The correct answer is c) cot θ.

Key Takeaways:

csc θ = 1/sin θ
sec θ = 1/cos θ
cot θ = 1/tan θ

Understanding these reciprocal identities is crucial for simplifying trigonometric expressions and solving equations.

Ratio trigonometric Identities

The fundamental ratio identities in trigonometry establish a direct connection between the tangent and cotangent functions and the sine and cosine functions. Specifically, the tangent of an angle, denoted as $\tan(\theta)$ , is defined as the ratio of the sine of that angle to its cosine, expressed mathematically as

$\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$ .

Conversely, the cotangent, $\cot(\theta)$ , which is the reciprocal of the tangent, can be expressed as

$\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)}$ .

These relationships are crucial for simplifying trigonometric expressions and solving equations.
Ratio trigonometric Identities: Solved Examples

Ratio trigonometric Identities Examples

Question 01: If $\sin(\theta) = \frac{3}{5}$ and $\cos(\theta) = \frac{4}{5}$ , find $\tan(\theta)$ .

Solution:

$\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$

$\tan(\theta) = \frac{\frac{3}{5}}{\frac{4}{5}}$

$\tan(\theta) = \frac{3}{5} \cdot \frac{5}{4}$

$\tan(\theta) = \frac{3}{4}$

Question 02: If $\tan(\theta) = \frac{1}{\sqrt{3}}$ , find $\cot(\theta)$ .

Solution:

$\cot(\theta) = \frac{1}{\tan(\theta)}$

$\cot(\theta) = \frac{1}{\frac{1}{\sqrt{3}}}$

$\cot(\theta) = \sqrt{3}$

Question 03: Simplify the expression $\frac{\sin(x)}{\cos(x)} \cdot \cot(x)$ .

Solution:

$\frac{\sin(x)}{\cos(x)} = \tan(x)$

$\tan(x) \cdot \cot(x) = \tan(x) \cdot \frac{1}{\tan(x)}$

$\tan(x) \cdot \frac{1}{\tan(x)} = 1$

Therefore, the simplified expression is 1.

Question 04: Prove that $\tan(\theta) \cdot \cos(\theta) = \sin(\theta)$ .

Solution:

Start with the left side: $\tan(\theta) \cdot \cos(\theta)$

Substitute $\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$ :

$\left(\frac{\sin(\theta)}{\cos(\theta)}\right) \cdot \cos(\theta)$

The $\cos(\theta)$ terms cancel out: $\sin(\theta)$

This equals the right side, so the identity is proven.

Pythagorean Identities

Pythagorean trigonometric identities are based on the Pythagorean theorem. There are three main Pythagorean trigonometric identities.

1. $\sin^2\theta + \cos^2\theta &= 1$

Alternative forms

$1 - \sin^2\theta &= \cos^2\theta$
$1 - \cos^2\theta &= \sin^2\theta$

2. $\sec^2\theta - \tan^2\theta &= 1$

Alternative forms

$\sec^2\theta &= 1 + \tan^2\theta$
$\sec^2\theta - 1 &= \tan^2\theta$

3. $\csc^2\theta - \cot^2\theta &= 1$

Alternative forms

$\csc^2\theta &= 1 + \cot^2\theta$
$\csc^2\theta - 1 &= \cot^2\theta$

Pythagorean Identities calculator

Opposite Angle Identities

$\sin(-\theta) &= -\sin \theta$
$\csc(-\theta) &= -\csc \theta$
$\cos(-\theta) &= \cos \theta$
$\sec(-\theta) &= \sec \theta$
$\tan(-\theta) &= -\tan \theta$
$\cot(-\theta) &= -\cot \theta$

Complementary Angle Identities

Complementary angles are two angles that add up to 90 degrees. The complement of an angle θ is (90 – θ). The relationships between the trigonometric functions of complementary angles are called co-function identities.

$\sin(90^\circ - \theta) &= \cos \theta$
$\cos(90^\circ - \theta) &= \sin \theta$
$\tan(90^\circ - \theta) &= \cot \theta$
$\csc(90^\circ - \theta) &= \sec \theta$
$sec(90^\circ - \theta) &= \csc \theta$
$\cot(90^\circ - \theta) &= \tan \theta$

Supplementary Angle Identities

Supplementary angles are two angles that add up to 180 degrees. The supplement of an angle θ is (180 – θ). Here are the trigonometric relationships for supplementary angles:

$\sin(180^\circ - \theta) &= \sin \theta$
$\cos(180^\circ - \theta) &= -\cos \theta$
$\tan(180^\circ - \theta) &= -\tan \theta$
$\csc(180^\circ - \theta) &= \csc \theta$
$sec(180^\circ - \theta) &= -\sec \theta$
$\cot(180^\circ - \theta) &= -\cot \theta$

Sum and Difference Identities

Sum and difference identities are formulas that express trigonometric functions of the sum or difference of two angles, such as $sin(\theta+\phi)$ , $cos(\theta-\phi)$ , and $tan(\theta+\phi)$ . These formulas are key tools in trigonometry

$\sin(\theta + \phi) &= \sin \theta \cos \phi + \cos \theta \sin \phi$
$\sin(\theta - \phi) &= \sin \theta \cos \phi - \cos \theta \sin \phi$
$\cos(\theta + \phi) &= \cos \theta \cos \phi - \sin \theta \sin \phi$
$\cos(\theta - \phi) &= \cos \theta \cos \phi + \sin \theta \sin \phi$
$\tan(\theta + \phi) &= \frac{\tan \theta + \tan \phi}{1 - \tan \theta \tan \phi}$
$\tan(\theta - \phi) &= \frac{\tan \theta - \tan \phi}{1 + \tan \theta \tan \phi}$

Periodic Identities

Trigonometric functions are periodic, meaning their values repeat at regular intervals. Periodic identities describe this repeating behavior. Here are the periodic identities for sine, cosine, and tangent.

$\sin(\theta + 2\pi k) &= \sin \theta$
$\cos(\theta + 2\pi k) &= \cos \theta$
$\tan(\theta + \pi k) &= \tan \theta$

Where k is any integer (k = 0, ±1, ±2, ±3, …).

Double Angle and Half Angle Identities

Double-angle formulas, derived from sum identities, express trigonometric functions of twice an angle. For example, substituting A = B = θ into sin(A+B) = sinAcosB + cosAsinB yields sin(2θ) = 2sinθcosθ. Other double-angle identities for cosine and tangent can be derived similarly.

other forms can be derived as

sin(2θ) = 2sin(θ)cos(θ)
cos(2θ) = cos²(θ) – sin²(θ)
cos(2θ) = 2cos²(θ) – 1
cos(2θ) = 1 – 2sin²(θ)
$\tan 2\theta &= \frac{2\tan\theta}{1 - \tan^2\theta}$

Half Angle Formulas: Using one of the above double-angle formulas,

$\cos 2\theta &= 1 - 2\sin^2\theta$
$2\sin^2\theta &= 1 - \cos 2\theta$
$\sin^2\theta &= \frac{1 - \cos 2\theta}{2}$
$\sin\theta &= \pm\sqrt{\frac{1 - \cos 2\theta}{2}}$

Replacing θ by θ/2 on both sides,

$\sin\left(\frac{\theta}{2}\right) = \pm\sqrt{\frac{1 - \cos\theta}{2}}$

Similarly,

$\sin\left(\frac{\theta}{2}\right) &= \pm\sqrt{\frac{1 - \cos\theta}{2}}$
$\cos\left(\frac{\theta}{2}\right) &= \pm\sqrt{\frac{1 + \cos\theta}{2}}$
$\tan\left(\frac{\theta}{2}\right) &= \pm\sqrt{\frac{1 - \cos\theta}{1 + \cos\theta}}$

Triple Angle trigonometric Identities

Triple angle identities connect trigonometric functions of 3θ to functions of θ. These identities express, for example, sin(3θ) in terms of sin(θ). One way to derive the triple angle formula for sine is by using the sum or addition formulas. Similar derivations exist for other triple angle identities.

We can write $sin 3x$ as:

$sin (3x) = sin (2x + x)$
$= sin 2x cos x + cos 2x sin x$

By using the double-angle formula of sine,
$sin 3x = 2 sin x cos x cos x + cos 2x sin x$

Using the Pythagorean identity and the double-angle formula for cosine…
2sin(x)(1 – sin²(x)) + (1 – 2sin²(x))sin(x)
= 2sin(x) – 2sin³(x) + sin(x) – 2sin³(x)
= 3sin(x) – 4sin³(x)

Just like, we can derive the other formulas as well.

$sin(3x) = 3sin(x) - 4sin3(x)$
$cos(3x) = 4cos3(x) - 3 cos x$
$tan(3x) = \frac{3 tan x - tan3x}{1 - 3tan2x}$

Sum and Product of trigonometric Identities

These trigonometric identities allow us to rewrite sums of trigonometric functions as products, and vice-versa, products as sums. This conversion is useful for simplifying expressions or solving trigonometric equations. They provide a bridge between addition and multiplication of these functions.

Sum to Product Identities: These identities are

$\sin A + \sin B &= 2\sin\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right)$
$\sin A - \sin B &= 2\cos\left(\frac{A + B}{2}\right)\sin\left(\frac{A - B}{2}\right)$
$\cos A + \cos B &= 2\cos\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right)$
$\cos A - \cos B &= -2\sin\left(\frac{A + B}{2}\right)\sin\left(\frac{A - B}{2}\right)$

Product to Sum Identities: These identities are

$\sin A \cos B &= \frac{1}{2}[\sin(A + B) + \sin(A - B)]$
$\cos A \cos B &= \frac{1}{2}[\cos(A + B) + \cos(A - B)]$
$\sin A \sin B &= \frac{1}{2}[\cos(A - B) - \cos(A + B)]$

Trigonometric Identities Proofs

Mastering trigonometric identities proofs is crucial for advanced mathematics and physics. These proofs involve manipulating trigonometric expressions using fundamental identities (like Pythagorean, reciprocal, and quotient identities) to demonstrate their equivalence. Skillful application of algebraic techniques, combined with a deep understanding of trigonometric relationships, enables the simplification and verification of complex equations, ultimately solidifying a robust foundation in trigonometry.

Download PDF proofs of Trigonometric Identities Proofs

Sine Law and Cosine Law

The trigonometric identities commonly studied are based on right triangles. However, some additional identities are necessary when working with triangles that don’t have a right angle. These additional formulas extend the application of trigonometry to a wider range of triangles.

Sine Rule:The sine rule relates the sides and angles of any triangle. For a triangle with sides a, b, and c, and opposite angles A, B, and C respectively, the sine rule states:

a/sin(A) = b/sin(B) = c/sin(C).

This can also be expressed as

sin(A)/a = sin(B)/b = sin(C)/c

or by comparing pairs of sides and angles, such as

a/b = sin(A)/sin(B)
b/c = sin(B)/sin(C)
c/a = sin(C)/sin(A)

Cosine Rule:The cosine rule relates the sides and angles of any triangle, often used when two sides and the angle between them are known. For a triangle with sides a, b, and c, and opposite angles A, B, and C, the cosine rule states:

a² = b² + c² – 2bccos(A)
b² = c² + a² – 2cacos(B)
c² = a² + b² – 2abcos(C)

Law of sines Calculator

Effortless Triangle Solutions: Instantly calculate unknown angles or side lengths in any triangle using the Law of Sines.
Versatile Application: Solve oblique triangles where standard right-angle trigonometry doesn’t apply.
Accuracy & Speed: Obtain precise results quickly, enhancing problem-solving efficiency.
Educational Tool: Ideal for students and professionals to verify calculations and deepen understanding.
User-Friendly Interface: Simple input and output for seamless calculations, regardless of mathematical expertise.

use law of sine calculator to find the values of trigonometric identities.

Example of Sine Law

Given a triangle ABC, if a = 4 units, A = 45 degrees, and B = 30 degrees, then find the length of b. Verify it using law of sine.

Solution:

$\frac{a}{\sin A}=\frac{b}{\sin B}$

$b = \frac{a \times \sin B}{\sin A}$

$b = \frac{4 \times \sin 30^\circ}{\sin 45^\circ}$

$b = \frac{4 \times \frac{1}{2}}{\frac{\sqrt{2}}{2}} = \frac{2}{\frac{\sqrt{2}}{2}} = \frac{4}{\sqrt{2}}$

$b = \frac{4}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}$

Example of Cosine Law

The sides of a triangle are given by a = 5, b = 4, c = 3. Find the value of the angle opposite to a and verify it using the law of cosine.

Solution:

$a^2 = b^2 + c^2 - 2bc \cos A$

$\cos A = \frac{b^2 + c^2 - a^2}{2bc}$

$\cos A = \frac{4^2 + 3^2 - 5^2}{2 \cdot 4 \cdot 3} = \frac{16 + 9 - 25}{24} = \frac{0}{24} = 0$

$A = \cos^{-1}(0)= 90^\circ$

Note: you can use sine calculator and cosine calculator to find the answers.

What are the 3 main trigonometric identities?

The main trigonometric identities are

Sin θ = 1/Csc θ or Csc θ = 1/Sin θ
Cos θ = 1/Sec θ or Sec θ = 1/Cos θ
Tan θ = 1/Cot θ or Cot θ = 1/Tan θ

What are the 7 trigonometric identities?

Here are the 7 trigonometric identities:

$sin^2(x) + cos^2(x) = 1$
$1 + tan^2(x) = sec^2(x)$
$1 + cot^2(x) = csc^2(x)$
$sin(x) = 1 / csc(x)$
$cos(x) = 1 / sec(x)$
$tan(x) = sin(x) / cos(x)$
$cot(x) = cos(x) / sin(x)$

What is the easiest way trick to remember trigonometry?

Utilize simple mnemonics, like 'SOH CAH TOA' for sine, cosine, and tangent ratios, and consistently practice applying them to solidify your understanding.

What are the trigonometric identities class 10th?

The trigonometric identities commonly covered in 10th grade include the Pythagorean identity, sin²θ + cos²θ = 1. Students also learn related identities such as 1 + tan²θ = sec²θ and 1 + cot²θ = cosec²θ. Reciprocal relationships like sin θ = 1/cosec θ, cos θ = 1/sec θ, and tan θ = 1/cot θ are also introduced. Finally, the quotient identity, tan θ = sin θ / cos θ, is a key component of 10th-grade trigonometry. These relationships are fundamental for solving trigonometric problems.

What are Trigonometry Identities used for?

Trigonometric identities are fundamental tools used to simplify and manipulate trigonometric expressions. They establish relationships between different trigonometric functions, allowing us to rewrite expressions in more convenient forms for solving equations, proving other identities, or evaluating complex functions. These identities are crucial in various fields like physics, engineering, and computer graphics, where trigonometric functions model periodic phenomena such as waves and oscillations. Ultimately, they provide a powerful means of analyzing and understanding relationships involving angles and their associated ratios.

Who is the father of trigonometry?

While the development of trigonometry was a gradual process with contributions from many mathematicians, Hipparchus of Nicaea, a Greek astronomer and mathematician, is often considered the "father of trigonometry" due to his systematic use of trigonometric tables and his significant contributions to its early development.

What are the 48 formulas of trigonometry class 10?

Here is the list of formas

sin A = Perpendicular/ Hypotenuse
cos A = Base/ Hypotenuse
tan A = Perpendicular/ Base
cos2 A + sin2 A = 1
1 + tan2 A = sec2 A
cot2 A + 1 = cosec2 A
sin(90∘−A) = cos A
cos(90∘−A) = sin A
tan(90∘−A) = cot A
cot(90∘−A) = tan A
sec(90∘−A) = cosec A
cosec(90∘−A) = sec A
sin² θ + cos² θ = 1
sin² θ = 1 – cos² θ
cos² θ = 1 – sin² θ
cosec² θ – cot² θ = 1
cosec² θ = 1 + cot² θ
cot² θ = cosec² θ – 1
sec² θ – tan² θ = 1
sec² θ = 1 + tan² θ
tan² θ = sec² θ – 1
sin θ cosec θ = 1
cos θ sec θ = 1
tan θ cot θ = 1

If you want to learn more details then click on link trigonometric-identities.