Locus of a complex number

by
Locus of complex number play a very important role in the complex analysis. Today we learn how to represent and find the locus of a complex number. We can also prepare Multiple choice questions about this topic and complex analysis.
         Let  P(Z) be the property that satisfied by a complex number  z = x + iy.
Let there is a complex number that may satisfy the condition |z| =2. Then the set  A = { z : |z| = 2 }
⇒  { ( x, y} : | z | = 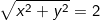 \fn_cm \small \fn_cm \small \sqrt{x^2+y^2} = 2   }
⇒   { ( x, y} : | z | = 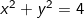 \fn_cm \small x^2 + y^2 = 4   }
is called the locus of the complex number z satisfying | z | =2.

From above the locus of complex number z represents a circle with the center at ( 0, 0 ) and radius r = 2.

 EXAMPLE: Find the locus of a complex number z = x + iy, such that for a fixed point  \fn_cm \small z_1= x_1 + i y_1 ,  |z-z1 |= a
Solution:
   As    A = { z ; |z-z1 | =a }
                 ⇒  { ( x, y} : | \fn_cm \small (x-x_1) + i (y-y_1)| = a }
                ⇒  { ( x, y} : \fn_cm \small \fn_cm \small (x-x_1) ^2+ i (y-y_1)^2 = a^2  }
which is a circle with center at \fn_cm \small z_1= (x_1, y_1) and radius r = a
EXAMPLE: Let \fn_cm \small z_1= x_1 + i y_1 be a fixed complex number. Find the locus of all complex number z = x + iy such that Arg(z-z1) = \fn_cm \small \frac{\pi}{4}
Solution:
We know that   \fn_cm \small z-z_1= (x-x_1)+ i (y-y_1).
First we find the argument of z

so   \fn_cm \small \theta = Arg(z-z_1)

          ⇒  \fn_cm \small Tan^{-1}\frac{y-y_1}{x-x_1}

        Because  Arg(z-z1) = \fn_cm \small \frac{\pi}{4}

So               \fn_cm \small Tan^{-1}\frac{y-y_1}{x-x_1} = \fn_cm \small \frac{\pi}{4}

And            \fn_cm \small \frac{y-y_1}{x-x_1}= Tan \frac{\pi}{4}   = 1

So,  x-x1= y-y1       or    x – y =  x1-y1

Leave a Comment